Diffusivity: Difference between revisions
From Glossary of Meteorology
No edit summary |
m (Rewrite with Template:Term and clean up) |
||
| Line 1: | Line 1: | ||
{{Term | |||
|Display title=diffusivity | |||
{{ | |Definitions={{Definition | ||
|Num=1 | |||
|Meaning=(''Also called'' coefficient of diffusion.) The ratio of the [[flux]] of a [[conservative property]] through a specified surface by [[turbulence]] to the [[gradient]] of the mean property normal to the surface. | |||
|Explanation=In the special case of [[isotropic turbulence]] and no mean motion the Fickian diffusion equation (or Fick's equation) takes the form <blockquote>[[File:ams2001glos-De23.gif|link=|center|ams2001glos-De23]]</blockquote>where ''K''<sub>''s''</sub> represents the diffusivity, ∇<sup>2</sup> is the [[Laplacian operator]], and [[File:ams2001glos-Dex05.gif|link=|ams2001glos-Dex05]] is the [[mean value|mean value]] of the property [[File:ams2001glos-Dex06.gif|link=|ams2001glos-Dex06]]. This equation describes decreasing [[File:ams2001glos-Dex07.gif|link=|ams2001glos-Dex07]] where the Laplacian is negative and increasing [[File:ams2001glos-Dex08.gif|link=|ams2001glos-Dex08]] where the Laplacian is positive. The general case is more complex. In the statically stable [[atmosphere]] or ocean, the horizontal [[scale of turbulence]] is much greater than the vertical scale and [[turbulent diffusion]] in the horizontal may greatly exceed [[diffusion]] in the vertical. On the other hand, in the case of [[buoyancy]], vertical diffusion may be greater than horizontal diffusion. <br/>''See also'' [[mixing]], [[eddy flux]], [[turbulence length scales]].<br/> Fleagle, R. G., and J. A. Businger 1980. An Introduction to Atmospheric Physics. 2d ed., Academic Press, . 64– 66. <br/> Hinze, J. O. 1975. Turbulence. 2d ed., McGraw–Hill, . 48–55. | |||
}} | |||
= | }} | ||
Latest revision as of 12:20, 27 March 2024
(Also called coefficient of diffusion.) The ratio of the flux of a conservative property through a specified surface by turbulence to the gradient of the mean property normal to the surface.
In the special case of isotropic turbulence and no mean motion the Fickian diffusion equation (or Fick's equation) takes the form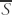 
is the mean value of the property 
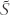. This equation describes decreasing 
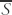where the Laplacian is negative and increasing 
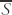where the Laplacian is positive. The general case is more complex. In the statically stable atmosphere or ocean, the horizontal scale of turbulence is much greater than the vertical scale and turbulent diffusion in the horizontal may greatly exceed diffusion in the vertical. On the other hand, in the case of buoyancy, vertical diffusion may be greater than horizontal diffusion.
See also mixing, eddy flux, turbulence length scales.
Fleagle, R. G., and J. A. Businger 1980. An Introduction to Atmospheric Physics. 2d ed., Academic Press, . 64– 66.
Hinze, J. O. 1975. Turbulence. 2d ed., McGraw–Hill, . 48–55.
where Ks represents the diffusivity, ∇2 is the Laplacian operator, and
is the mean value of the property . This equation describes decreasing where the Laplacian is negative and increasing where the Laplacian is positive. The general case is more complex. In the statically stable atmosphere or ocean, the horizontal scale of turbulence is much greater than the vertical scale and turbulent diffusion in the horizontal may greatly exceed diffusion in the vertical. On the other hand, in the case of buoyancy, vertical diffusion may be greater than horizontal diffusion. See also mixing, eddy flux, turbulence length scales.
Fleagle, R. G., and J. A. Businger 1980. An Introduction to Atmospheric Physics. 2d ed., Academic Press, . 64– 66.
Hinze, J. O. 1975. Turbulence. 2d ed., McGraw–Hill, . 48–55.
