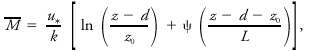Aerodynamic roughness length: Difference between revisions
(Created page with " {{TermHeader}} {{TermSearch}} <div class="termentry"> <div class="term"> == aerodynamic roughness length == </div> <div class="definition"><div class="short_definition...") |
m (Rewrite with Template:Term and clean up) |
||
| (4 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
== aerodynamic roughness length == | == aerodynamic roughness length == | ||
(''Also called'' the roughness length ''z''<sub>0</sub>.) The height above the displacement plane at which the mean wind becomes zero when extrapolating the logarithmic [[wind speed]] [[profile]] downward through the [[surface layer]].<br/> | |||
It is a theoretical height that must be determined from the wind speed profile, although there has been some success at relating this height to the arrangement, spacing, and physical height of individual roughness elements such as trees or houses. The average wind speed [[File:ams2001glos-Aex02.gif|link=|ams2001glos-Aex02]] in the surface layer can be written using [[Monin-obukhov similarity theory|Monin–Obukhov similarity theory]] as <blockquote>[[File:ams2001glos-Ae12.gif|link=|center|ams2001glos-Ae12]]</blockquote> where ''z'' is height above ground, ''d'' is height of the displacement plane above ground, ''L'' is the Monin–Obukhov length [[scale]], ''k'' is [[von Kármán's constant]], ψ is a [[stability]] correction factor (=0 for statically neutral conditions), and ''u''<sub>*</sub> is the [[friction velocity]]. To determine aerodynamic roughness, most experimentalists prefer to make [[wind profile]] measurements during statically neutral conditions (windy, [[overcast]], negligible [[temperature]] [[advection]]) so that ψ = 0 in the equation above. <br/>''Compare'' [[Charnock's relation]].<br/> | |||
<p>''Term edited 25 September 2019.''</p> | |||
Latest revision as of 21:21, 27 March 2024
aerodynamic roughness length
(Also called the roughness length z0.) The height above the displacement plane at which the mean wind becomes zero when extrapolating the logarithmic wind speed profile downward through the surface layer.
It is a theoretical height that must be determined from the wind speed profile, although there has been some success at relating this height to the arrangement, spacing, and physical height of individual roughness elements such as trees or houses. The average wind speed 
in the surface layer can be written using Monin–Obukhov similarity theory as
where z is height above ground, d is height of the displacement plane above ground, L is the Monin–Obukhov length scale, k is von Kármán's constant, ψ is a stability correction factor (=0 for statically neutral conditions), and u* is the friction velocity. To determine aerodynamic roughness, most experimentalists prefer to make wind profile measurements during statically neutral conditions (windy, overcast, negligible temperature advection) so that ψ = 0 in the equation above.
Compare Charnock's relation.
Term edited 25 September 2019.
