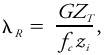Rossby radius of deformation: Difference between revisions
From Glossary of Meteorology
(Created page with " {{TermHeader}} {{TermSearch}} <div class="termentry"> <div class="term"> == Rossby radius of deformation == </div> #<div class="definition"><div class="short_definitio...") |
m (Rewrite with Template:Term and clean up) |
||
| (2 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
{{Term | |||
|Display title=Rossby radius of deformation | |||
{{ | |Definitions={{Definition | ||
|Num=1 | |||
|Meaning=#The distance that cold pools of air can spread under the influence of the [[Coriolis force]]. | |||
|Explanation=A [[cold pool]] will initially spread out toward and under warmer air because of higher [[pressure]] under the cold, denser air. However, as the spreading [[velocity]] increases, the Coriolis force will increasingly turn the velocity vector until it is parallel, rather than perpendicular, to the [[pressure gradient|pressure gradient]]. At this point, no further spreading will occur and the winds will be in [[geostrophic equilibrium|geostrophic equilibrium]]. The final [[equilibrium]] distance traveled by the edge of the cold air equals the [[external Rossby radius of deformation|external Rossby radius of deformation]], λ<sub>''R''</sub>: <blockquote>[[File:ams2001glos-Re46.gif|link=|center|ams2001glos-Re46]]</blockquote> where ''g'' is gravitational [[acceleration]], ''H'' is the initial depth of the cold pool, Δθ is the [[potential temperature|potential temperature]] contrast between the cold and surrounding warm air, θ<sub>0</sub> is the [[absolute]] potential temperature of the warm air, and ''f''<sub>''c''</sub> is the [[Coriolis parameter]].<br/> | |||
#An internal Rossby radius of deformation can be defined for fluids with a [[gradient]] of [[potential temperature]] rather than a [[temperature]] interface: <blockquote>[[File:ams2001glos-Re47.gif|link=|center|ams2001glos-Re47]]</blockquote> where ''N''<sub>''BV''</sub> is the average [[Brunt–Väisälä frequency]] within the [[troposphere]] and ''Z''<sub>''T''</sub> is the depth of the troposphere.<br/> This radius is important for determining the [[phase speed]] and [[wavelength]] of [[baroclinic waves]] ([[Rossby waves]]) in the [[general circulation]]. An alternative definition for internal Rossby radius of deformation is <blockquote>[[File:ams2001glos-Re48.gif|link=|center|ams2001glos-Re48]]</blockquote> where ''G'' is the [[geostrophic wind]] speed and ''z''<sub>''i''</sub> is the depth of the [[atmospheric boundary layer]], approximated here as ''z''<sub>''i''</sub> = ''G''/''N''<sub>''BV''</sub>. This form is useful in determining boundary layer (Ekman) pumping through the top of the [[boundary layer]]. | |||
}} | |||
}} | |||
# | |||
# | |||
Latest revision as of 08:42, 27 March 2024
- The distance that cold pools of air can spread under the influence of the Coriolis force.
where g is gravitational acceleration, H is the initial depth of the cold pool, Δθ is the potential temperature contrast between the cold and surrounding warm air, θ0 is the absolute potential temperature of the warm air, and fc is the Coriolis parameter.
- An internal Rossby radius of deformation can be defined for fluids with a gradient of potential temperature rather than a temperature interface:
where NBV is the average Brunt–Väisälä frequency within the troposphere and ZT is the depth of the troposphere.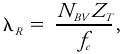
This radius is important for determining the phase speed and wavelength of baroclinic waves (Rossby waves) in the general circulation. An alternative definition for internal Rossby radius of deformation is
where G is the geostrophic wind speed and zi is the depth of the atmospheric boundary layer, approximated here as zi = G/NBV. This form is useful in determining boundary layer (Ekman) pumping through the top of the boundary layer.